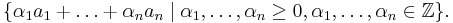Hilbert basis (linear programming)
In linear programming, a Hilbert basis for a convex cone C is an integer cone basis: minimal set of integer vectors such that every integer vector in C is a conical combination of the vectors in the Hilbert basis with integer coefficients.
Definition
A set  of integer vectors is a Hilbert basis if every integer vector in its convex cone
of integer vectors is a Hilbert basis if every integer vector in its convex cone
is also in its integer cone
References
- Bruns, Winfried; Gubeladze, Joseph; Henk, Martin; Martin, Alexander; Weismantel, Robert (1999), "A counterexample to an integer analogue of Carathéodory's theorem", Journal für die reine und angewandte Mathematik 510 (510): 179–185, doi:10.1515/crll.1999.045
- Cook, William John; Fonlupt, Jean; Schrijver, Alexander (1986), "An integer analogue of Carathéodory's theorem", Journal of Combinatorial Theory. Series B 40 (1): 63–70, doi:10.1016/0095-8956(86)90064-X
- Eisenbrand, Friedrich; Shmonin, Gennady (2006), "Carathéodory bounds for integer cones", Operations Research Letters 34 (5): 564–568, doi:10.1016/j.orl.2005.09.008
- D. V. Pasechnik (2001). "On computing the Hilbert bases via the Elliott—MacMahon algorithm". Theoretical Computer Science 263: 37–46. doi:10.1016/S0304-3975(00)00229-2.